Le coefficient de détermination, noté R2R^2R2, est une mesure statistique qui évalue la proportion de la variance dans la variable dépendante qui est prédite à partir de la variable indépendante. Il est couramment utilisé pour évaluer la qualité d’un modèle de régression.
Formule
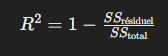
Explication
- SSreˊsiduelSS_{\text{résiduel}}SSreˊsiduel : somme des carrés des résidus (différence entre les valeurs observées et les valeurs prédites)
- SStotalSS_{\text{total}}SStotal : somme des carrés totaux (différence entre les valeurs observées et la moyenne des valeurs observées)
Interprétation
- R2R^2R2 varie entre 0 et 1.
- R2=1R^2 = 1R2=1 : le modèle explique parfaitement la variance des données.
- R2=0R^2 = 0R2=0 : le modèle n’explique aucune variance des données.
- Un R2R^2R2 proche de 1 indique un modèle prédictif fort.
- Un R2R^2R2 proche de 0 indique que le modèle ne parvient pas à expliquer la variance des données.
Exemple
Supposons que vous ayez les valeurs observées suivantes : [3, 5, 2.5, 7] et les valeurs prédites suivantes : [2.5, 5, 4, 8].

Donc, R2=0.7241R^2 = 0.7241R2=0.7241, ce qui signifie que le modèle explique environ 72.41% de la variance des données observées.
Utilisation
Le R2R^2R2 est souvent utilisé en apprentissage automatique et en analyse de régression pour évaluer la performance des modèles. Cependant, il est important de noter que R2R^2R2 ne peut pas diminuer avec l’ajout de variables explicatives, ce qui peut parfois mener à une fausse impression de meilleure performance.
0 commentaire